Answer:
c) 2i, 6, -6
Explanation:
The given function is
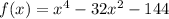
The given zero to this function is
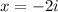
Remember that a function has so many roots as its grade dictates. So, in this case, the function grade is four, which means it has four solutions.
Now, the given function is an imaginary number, which happens in pairs, that means the second root must be
 , because a function can have complex roots as pairs, 2, 4, 6,... many solutions.
, because a function can have complex roots as pairs, 2, 4, 6,... many solutions.
The other two solutions are 6 and -6, because if we replace them into the function, it will give zero.
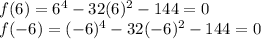
Therefore, the other three solutions missing are: c) 2, 6, -6.
(The image attached shows the real solutions).