Question

How would you use the Fundamental Theorem of Calculus to determine the value(s) of b if the area under the graph g(x)=4x between x=1 and x=b is equal to 240?

Answer 1

`\displaystyle b = 11`

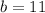
General Formulas and Concepts:

Pre-Algebra

Order of Operations: BPEMDAS

1. Brackets
2. Parenthesis
3. Exponents
4. Multiplication
5. Division
6. Addition
7. Subtraction

• Left to Right

Equality Properties

• Multiplication Property of Equality
• Division Property of Equality
• Addition Property of Equality
• Subtraction Property of Equality

Algebra I

Functions

• Function Notation

Calculus

Integration

• Integrals
• Definite Integrals
• Integration Constant C

Integration Rule [Reverse Power Rule]:
`\displaystyle \int {x^n} \, dx = (x^(n + 1))/(n + 1) + C`

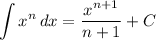
Integration Rule [Fundamental Theorem of Calculus 1]:
`\displaystyle \int\limits^b_a {f(x)} \, dx = F(b) - F(a)`

Integration Property [Multiplied Constant]:
`\displaystyle \int {cf(x)} \, dx = c \int {f(x)} \, dx`

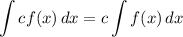
Area of a Region Formula:
`\displaystyle A = \int\limits^b_a {[f(x) - g(x)]} \, dx`

Explanation:

Step 1: Define

Identify

g(x) = 4x

Interval [1, b]

A = 240

Step 2: Solve for b

1. Substitute in variables [Area of a Region Formula]:
   `\displaystyle \int\limits^b_1 {4x} \, dx = 240`
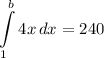
2. [Integral] Rewrite [Integration Property - Multiplied Constant]:
   `\displaystyle 4\int\limits^b_1 {x} \, dx = 240`
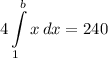
3. [Integral] Integrate [Integration Rule - Reverse Power Rule]:
   `\displaystyle 4((x^2)/(2)) \bigg| \limits^b_1 = 240`
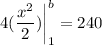
4. Evaluate [Integration Rule - Fundamental Theorem of Calculus 1]:
   `\displaystyle 4((b^2)/(2) - (1)/(2)) = 240`
5. [Distributive Property] Distribute 4:
   `\displaystyle 2b^2 - 2 = 240`
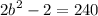
6. [Addition Property of Equality] Add 2 on both sides:
   `\displaystyle 2b^2 = 242`
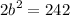
7. [Division Property of Equality] Divide 2 on both sides:
   `\displaystyle b^2 = 121`
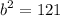
8. [Equality Property] Square root both sides:
   `\displaystyle b = \pm 11`
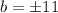
9. Choose:
   `\displaystyle b = 11`

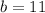
Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Integration

Book: College Calculus 10e