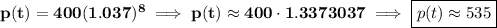well, for the current price today, let's see, not even one day has passed, to we don't have a "t" value that's greater than 0, so since today 0years and 0days and 0seconds have passed, t =0

now, 8 years from now, well, 8 years would had passed by then, t = 8