Question

an airplane is flying from montreal to vancouver. the wind is blowing from the west at 60km/h. the airplane flies at an airspeed of 750km/h and must stay on a heading of 65 degrees west of north. what heading should the pilot take to compensate for the wind? what is the speed of the airplane relative to the ground?

Answer 1

Refer to the diagram shown below.

In order for the airplane to maintain a heading of 65° west of north, it actually heads at (65° +x) west of north at a speed of 750 km/h, to compensate for the wind blowing from west t east at 60 km/h.

The actual speed of the airplane relative to the ground is V km/h.

From geometry, obtain the triangle shown.
The speed of 750 km/h is opposite an angle of 155°, and the unknown angle x is opposite the wind speed of 60 km/h.

From the Law of Sines, obtain

`(sin(x))/(60)= (sin(155^(o))/(750) \\ sin(x)= ((60)/(750))sin(155^(o))=0.0338`

`x=sin^(-1)0.0338=1.937^(o)`

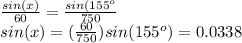
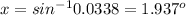
The heading that the pilot should take is 65 + 1.937 = 66.94° west of north.

The third angle of the triangle is 180 - (155 + 1.937) = 23.063°.
Use the Law of Sines to calculate V.

`(V)/(sin(23.063^(o)))= (750)/(sin(155^(o)))`

`V=( (sin(23.063))/(sin(155)) )750=695.21\,km/h`

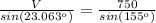
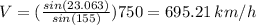
Answer:
The pilot heads approximately 67° (nearest integer) west of north.
The speed of the airplane relative to ground is 695.2 km/h (nearest tenth)