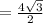Question

The lengths of the sides of a right triangle are a and b, and the hypotenuse is

c. find the area of the triangle. a=2 squareroot 3; c=4 a = sq. ft.

Answer 1

a^2+b^2=c^2
(2sqrt3)^2+b^2=16
12+b^2=16
solve for b
b=2
Now triangle area is A=1/2 bh
so
A=(1/2)(2)(2sqrt3)
A=2sqrt3

Answer 2

Area is 2√3 ft².

Explanation:

Given,

A right triangle having sides,

a = 2√3 ft,

c = 4 ft,

Where, c is the hypotenuse of the triangle,

If b is the other leg of the triangle,

By the pythagorean theorem,

`c^2=a^2+b^2`

`4^2=(2√(3))^2+b^2`

`16=12+b^2`

`4=b^2`

`\implies b = 2`

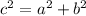
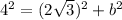
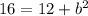
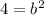
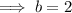
Hence, the area of the given triangle is,

`A=(1)/(2)* a* b`

`=(1)/(2)* 2√(3)* 2`

`=(4√(3))/(2)`

`=2√(3)\text{ square ft}`