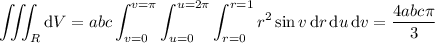Question

(6) (Bonus question: worth 10 points. Total points for assignment not to exceed 100.) Use an iterated integral to compute the volume of the ellipsoid x^2/a^2 + y^2/b^2 + z^2/c^2 = 1. The a, b, and c are positive constants.

Answer 1

Let
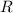
`R` be the ellipsoid with equation


`\left(\frac xa\right)^2+\left(\frac yb\right)^2+\left(\frac zc\right)^2=1`

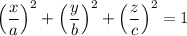
so that the volume of
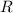
`R` is given by the triple integral


`\displaystyle\iiint_R\mathrm dV`

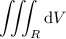
Consider the augmented spherical coordinates given by the identities


`\begin{cases}x=ar\cos u\sin v\\y=br\sin u\sin v\\z=cr\cos v\end{cases}`

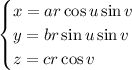
Computing the Jacobian, we find that the volume element is given by


`\mathrm dV=\mathrm dx\,\mathrm dy\,\mathrm dz=abcr^2\sin v\,\mathrm dr\,\mathrm du\,\mathrm dv`

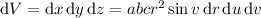
so that the volume integral can be written as


`\displaystyle\iiint_R\mathrm dV=abc\int_(v=0)^(v=\pi)\int_(u=0)^(u=2\pi)\int_(r=0)^(r=1)r^2\sin v\,\mathrm dr\,\mathrm du\,\mathrm dv=\frac{4abc\pi}3`