The given expression is
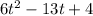
To factor this expression, first, we use the quadratic formula.
![t=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/d921kixtd11xsbpq2gng.png)
Where a = 6, b = -13, and c = 4.
Always remember that a is the coefficient of the square variable, b is the coefficient of the linear variable, and c is the constant term (without any variable).
Let's use these values in the formula.
![\begin{gathered} t=\frac{-(-13)\pm\sqrt[]{(-13)^2-4\cdot6\cdot4}}{2\cdot6} \\ \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/bt0gbep4nh3056u0iwd0.png)
Let's solve
![t=\frac{13\pm\sqrt[]{169-96}}{12}=\frac{13\pm\sqrt[]{73}}{12}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/o0dwg7isqj64mreph2bc.png)
Remember that the square root always has two solutions.
![\begin{gathered} t_1=\frac{13+\sqrt[]{73}}{12} \\ t_1=\frac{13-\sqrt[]{73}}{12} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/9lw0cc0a1rya4hlzjcxr.png)
However, we have to write these expressions as factors, as follows
![\begin{gathered} t-\frac{13+\sqrt[]{73}}{12} \\ t-\frac{13-\sqrt[]{73}}{12} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/ptaaxszrkmumfahhhmf3.png)
Therefore, the factored expression is
![(t-\frac{13+\sqrt[]{73}}{12})(t-\frac{13-\sqrt[]{73}}{12})](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/1qjw34as9rlgo2wqrey8.png)
At last, it's important to know that prime polynomials are irreducible polynomials, this means the polynomial cannot be factored by usual means, like in this case, we couldn't factor the polynomial using factoring strategies and we used the quadratic formula to do so.
Therefore, this polynomial counts as prime because there are no integers that fit.