Answer:
D. 99.9936%.
Explanation:
We have been given that the length of a screw produced by a machine is normally distributed with a mean of 0.65 inches and a standard deviation of 0.01 inches.
To find the percent of screws that are between 0.61 and 0.69 inches, first of we will find z-score for our given raw scores using z-score formula.
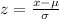 , where,
, where,
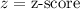 ,
,
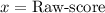 ,
,
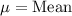 ,
,
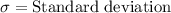 .
.
Now let us find z-score corresponding to our given raw scores.
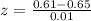
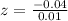
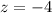
Now let us find z-score for raw score 0.69.
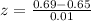
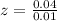
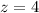
Now we will use formula to find the probability between two z-score as:
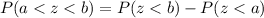
Upon substituting our given values in above formula we will get,
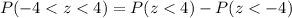
Using normal distribution table we will get,
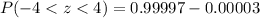
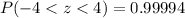
Now let us convert our answer into percent by multiplying 0.99994 by 100.
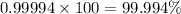
Therefore, 99.994% of screws are between 0.61 and 0.69 inches and option D is the correct choice.