Question

Find the possible value or values of n in the quadratic equation 2n2 – 7n + 6 = 0

Answer 1

2n^2-7n+6=0

2n^2-4n-3n+6=0

2n(n-2)-3(n-2)=0

(2n-3)(n-2)=0

n=3/2, n=2

Answer 2

`n=(3)/(2),\,\,n=2`.

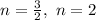Explanation:

The equation you have is a quadratic equation because the polynomial
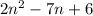`2n^(2)-7n+6` has degree 2. One of the methods available to solve kind of equations is to factorize the polynomial on the left hand side. To factorize you can do the following:

(1)
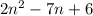`2n^2-7n+6`. The given polinomial

(2)
`(2*(2n^2-7n+6))/(2)=((2n)^(2)-7(2n)+12)/(2)`. Multiply and divide by 2, because it is the coeficient of
`n^(2)`

(3)
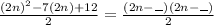`((2n)^(2)-7(2n)+12)/(2)=((2n-\_\_)(2n-\_\_))/(2)`. Separate the polynomial in two factors, each one with
`2n` as a first term. The sign in the first factor is equal to the sign in the second term of the polynomial, that is to say,
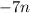`-7n`. The sign in the second factor is the sign of the second term multiplied by the sign of the third term, that is to say
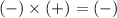`(-)*(+)=(-)` . In the blanks you should select two numbers whose sum is 7 and whose product is 12. Those numbers must be 3 and 4.

(4)The polynomial factorized is
`((2n-4)(2n-3))/(2)`

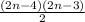
(5)Use the common factor in the numerator to cancel the number 2 in the denominator to obtain
`(n-2)(2n-3)`

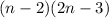
Then the given equation can be written as:

`{(2n-3)(n-2)=0`

The product of two expression equals zero if and only if one of the expression is zero. From here we have that

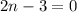`2n-3=0` or
`n-2=0`

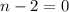
From the first equality we obtain that
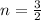`n=(3)/(2)`. From the second equality we obtain that
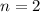`n=2`.