Answer:
x= -6 is the point of discontinuity.
Explanation:
We have been given the expression
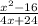
The first thing to find the discontinuity is to factorize the given rational function:
After factorization we get:
We will use
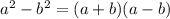
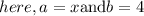 we will get:
we will get:
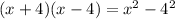
we will get:
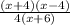
Discontinuity is the point where value of the function becomes not defined
Here, the point of discontinuity is -6 because when denominator becomes zero. function becomes not defined.
It has vertical asymptote but function is not defined.
Hence it is the point of discontinuity.