Question

How many solutions does this linear equation have? Y= 2x - 5

-8x - 4y = -20

Please only answer if you know.

Answer 1

y = 2x - 5...slope = 2, y int = -5

-8x - 4y = -20
-4y = 8x - 20
y = -2x + 5....slope = -2, y int = 5

different slopes, different y int's means 1 solution <==

** same slope, same y int = infinite solutions
** same slope, different y int's = no solutions

Answer 2

Our given system has exactly one solution.

Explanation:

We have been given a system of equation. We are asked to find the number of solutions for our given system.

First of all, we will convert our second equation in slope-intercept form of equation as shown below:

`-8x-4y=-20`

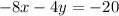
Upon dividing both sides of our equation by -4, we will get:

`(-8x)/(-4)-(4y)/(-4)=(-20)/(-4)`

`2x+y=5`

`2x-2x+y=-2x+5`

`y=-2x+5`

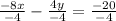
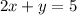
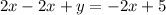
Upon comparing our both equations, we can see that they have different slopes and different y-intercepts, therefore, they will have exactly one solutions as they will intersect at one place.

Upon looking at our attachment, we can see that our explanation is correct.