Question

If you were to add all odd numbers between 1 and 11 (both inclusive), the result would be

Answer 1

The sequence of all odd numbers between 1 and 11 (both inclusive) is
1,3,5,7,9,11

This is an arithmetic sequence with common difference of d=2
The first term is a₁=1.

The number of the term 11 (without counting) is found from
1 + (n-1)*2 = 11
1 + 2n - 2 = 11
2n -1 = 11
2n = 12
n = 6

The sum of the first n terms of an arithmetic sequence is

`S_(n) = (n(a_(1)+a_(n)))/(2)`

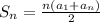
Therefore, the sum of the sequence is
S₆ = [6*(1 + 11)]/2
= (6*12)/2
= 36

Answer: 36