Question

Guess the value of the limit (correct to six decimal places). (if an answer does not exist, enter dne.) lim hâ0 (4 + h)5 â 1024 h

Answer 1

`\displaystyle\lim_(h\to0)\frac{(4+h)^5-1024}h=\lim_(h\to0)\frac{(4+h)^5-4^5}h`

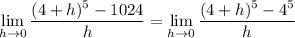
Recall the definition of the derivative of a function
`f(x)` at a point
`x=c`:


`f'(c)=\displaystyle\lim_(h\to 0)\frac{f(c+h)-f(c)}h`

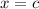
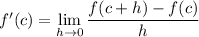
We can then see that
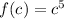
`f(c)=c^5`, and by the power rule we have
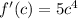
`f'(c)=5c^4`. Then replacing
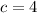
`c=4`, we arrive at


`\displaystyle\lim_(h\to0)\frac{(4+h)^5-4^5}h=5*4^4=1280`

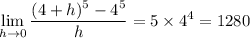
Alternatively, we could have expanded the binomial, giving


`\frac{(4+h)^5-4^5}h=\frac{(4^5+5*4^4h+10*4^3h^2+10*4^2h^3+5*4h^4+h^5)-4^5}h`

`=\frac{1280h+640h^2+160h^3+20h^4+h^5}h`

`=1280+640h+160h^2+20h^3+h^4`

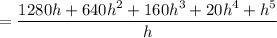
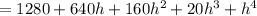
and so as
`h\to0` we're left with 1280, as expected.