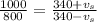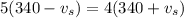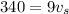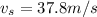Question

You stand by the railroad tracks as a train passes by. you hear a 1 000-hz frequency when the train approaches, which changes to 800 hz as it goes away. how fast is the train moving? the speed of sound in air is 340 m/s.

Answer 1

This is a concrete example of the Doppler effect. This effect is the change of frequency experienced by the listener or the observer with respect to their relative distance to the source of the sound. There can be two equations to be applied: to the approaching source, and to the receding source.

Approaching source:
frequency observed = [v/(v-v,source)]*frequency of source, where v is the velocity of sound . Substituting,
1000 = [340/(340-v,source)]*frequency of source <---- equation 1

Receding source:
frequency observed = [v/(v+v,source)]*frequency of source, where v is the velocity of sound . Substituting,
800 = [340/(340+v,source)]*frequency of source <---- equation 2

Rearranging equation 1: [1000(340-v,source)]/340 = frequency of source
Equation 2: 800 = [340/(340+v,source)]*frequency of source

Substituting equation 1 to equation 2:
800 = [340/(340+v,source)]*[1000(340-v,source)]/340

Solving using the scientific calculator under shift-solve feature,
v,source = 37.78 m/s

Therefore, the train is moving at 37.78 m/s.

Answer 2

`v_s= 37.8 m/s`

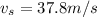
Step-by-step explanation:

As per Doppler's effect when source and observer moves relative to each other then the frequency of the sound observed is different from the real frequency

When source is moving towards the stationary observer then we have

`f_1 = f_o((v)/(v - v_s))`

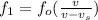
now when source of sound moving away from stationary observer then we have

`f_2 = f_o((v)/(v + v_s)`

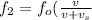
now from above two equations

`(f_1)/(f_2) = (v + v_s)/(v - v_s)`

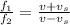
here we know that

`f_1 = 1000 hz`

`f_2 = 800 hz`

v = 340 m/s

now we have

`(1000)/(800) = (340 + v_s)/(340 - v_s)`

`5(340 - v_s) = 4(340 + v_s)`

`340 = 9 v_s`

`v_s = 37.8 m/s`