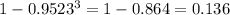Question

The probability of a randomly selected car crashing during a year in a certain country is 0.04770.0477. if a family has threethree ​cars, find the probability that at least one of them has a car crash during a year. is there any reason why the probability might be​ wrong?

Answer 1

P(having one crash) = 0.0477
P(having NO crash) = 1- 0.0477 = 0.9523

ⁿCₓ(p)ˣ. (1-p)ⁿ⁻ˣ
n= number of cars
x = number of crashes
p = 0.0477 (1 crash)
1-p = 0.9523 (NO crash:
Probability of NO crashes at all:

³C₀(0.0477)⁰(0.9523)⁽³⁻⁰⁾

³C₀(1)(0.9523)³ = 0.9523³ = 0.8636 Then P(NO CRASH) = 0.8636

P(at LEAST one crash) = 1 - 0.8636

P(at LEAST one crash) = 0.136

Answer 2

Probability questions asking for "at least one", are generally much easier to solve by finding the probability of the complement event, that is "none", and then subtracting from 1.

So we are going to find P(none of the cars crashes), then we will subtract it from 1, since:

P(at least one car crashes)+P(no car crashes)=1, as they are 2 disjoint complement events, either one or the other will happen, so the probability that either one or the other happens is 1.

P(a car not crashing)=1-0.0477=0.9523

P(car 1 not crash, car 2 not crash, car 3 not crash)=
`0.9523^(3)= 0.864`

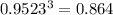
P(at least 1 of the cars crashes)=1-P(none of the 3 cars crash)=
`1-0.9523^(3)=1-0.864=0.136`