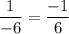Question

Calculus AB

lim x-->4 sqrt(x+5)-3 / 4-x
The answer is apparently -1/6
How do you solve this

Answer 1

assuming you mean

`\lim_(x \to 4) (√(x+5)-3)/(4-x)`

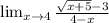
that means as x approaches 4

if we sub 0 for x we get
0/0
and intermitent form
use l'hopital's rule

so
take the derivitive of the top and bottom seperatly
l'hopitals rule is something like
if
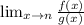
`\lim_(x \to n) (f(x))/(g(x))` results in 0/0 or -∞/∞ or∞/∞ then keep doing it until f(n)/g(n) gives a form that isn't intermitent

so

take derivitive of top and bottom

`((1)/(2√(x+5)))/(-1)`
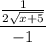
now, if we subsitute 4 for x we get

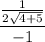
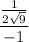
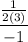
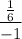
`((1)/(2√(4+5)))/(-1)`=


`((1)/(2√(9)))/(-1)`=


`((1)/(2(3)))/(-1)`=


`((1)/(6))/(-1)`=


`(1)/(-6)=(-1)/(6)`