Question

Solve the inequality. Check your solutions.

7−(2/b)<(5/b)

im not surehow to answer this, it's supposedly in a number form but I'mcompetely lost. Maybe a _

Answer 1

The inequality is


`7- (2)/(b)\ \textless \ (5)/(b)`

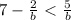
write 7 as 7b/b to have all the expressions in common denominator:


`(7b)/(b) - (2)/(b)\ \textless \ (5)/(b)`


`(7b-2)/(b) \ \textless \ (5)/(b)`


`(7b-2)/(b)- (5)/(b)\ \textless \ 0`


`(7b-2-5)/(b)\ \textless \ 0`


`(7b-7)/(b)\ \textless \ 0`


`(7(b-1))/(b)\ \textless \ 0`

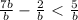
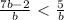
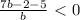
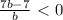
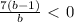
here b=1 is a root and b=0 is not in the domain of the expression, but it still has an effect in the sign of the expression.

the sign table of
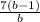
`(7(b-1))/(b)` is :

+++++++[0] --------[1] +++++

this means that for values of b to the left of 0 and to the right of 1, the expression is positive, and for values of b in (0, 1), the expression is negative.

that is
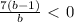
`(7(b-1))/(b)\ \textless \ 0` for b∈(0, 1)

Answer: (0, 1)