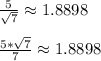Question

Explain why rationalizing the denominator does not change the value of the original expression

Answer 1

Rationalizing is just simpllifying, so the simplified value has the same value as the original expression.

Answer 2

Because basically, you are multiplying by 1

Explanation:

Let me explain this with an example. Rationalize the following expression:

`(5)/(√(7) )`

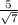
In order to rationalize the denominator, the numerator and denominator of the fraction must be multiplied by the root of the denominator. So, what happen if you do that? Well first of all you aren't altering the expression because:

`(√(7) )/(√(7) ) =1`

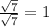
Right? Because a certain quantity divided by itself is always equal to 1. So basically you are doing this because you want to rewrite the expression without altering its original value, it is the same when you do this:

`9=3^2=3+3+3=√(81)`

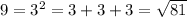
Therefore, the only thing you do when you rationalize is remove radicals from the denominator of a fraction. Take a look:

`(5)/(√(7) ) *(√(7) )/(√(7) ) =(5*√(7) )/(√(7)*√(7) ) =(5*√(7))/((√(7) )^2) =(5*√(7) )/(7)`

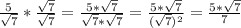
You can check this new expression is equal to the original using a calculator:

`(5)/(√(7) ) \approx1.8898\\\\(5*√(7) )/(7) \approx1.8898`