Question

Mateo is studying a human hair with a diameter of 6.5 x 10^-4 inches and a horse hair with a diameter of 1.3 x 10^-3 inches. Which statement is true?

A.The horse hair is 2 times as thick as the human hair.

B.The horse hair is 5 times as thick as the human hair

C.The human hair is 2 times as thick as the horse hair

D.The human hair is 5 times as thick as the horse hair

Answer 1

`\cfrac{1.3*10^(-3)}{6.5*10^(-4)}= 0.2*10^1=2`

A.The horse hair is 2 times as thick as the human hair.

Answer 2

A.The horse hair is 2 times as thick as the human hair.

Explanation:

We have been given that Mateo is studying a human hair with a diameter of
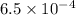`6.5* 10^(-4)` inches and a horse hair with a diameter of
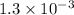`1.3* 10^(-3)` inches.

Since proportions states that two fractions are equal, So we will use proportions to solve our given problem.

`\frac{\text{Diameter of horse hair}}{\text{Diameter of human hair}}=(1.3* 10^(-3))/(6.5* 10^(-4))`

`\text{Diameter of horse hair}=(1.3* 10^(-3))/(6.5* 10^(-4))* \text{Diameter of human hair}`

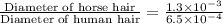
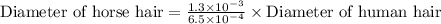
Now we will quotient rule of exponents to simplify our given problem.

`\text{Diameter of horse hair}=(1.3* 10^(-3--4))/(6.5)* \text{Diameter of human hair}`

`\text{Diameter of horse hair}=(1.3* 10^(-3+4))/(6.5)* \text{Diameter of human hair}`

`\text{Diameter of horse hair}=(1.3* 10^(1))/(6.5)* \text{Diameter of human hair}`

`\text{Diameter of horse hair}=(13)/(6.5)* \text{Diameter of human hair}`

`\text{Diameter of horse hair}=2* \text{Diameter of human hair}`

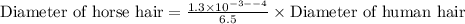
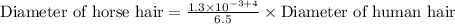
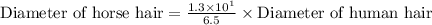
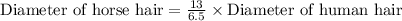
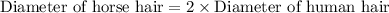
We can see that the diameter of horse hair is 2 times the diameter of human hair. Therefore, the horse hair is 2 times as thick as the human hair and option A is the correct choice.