Answer:
A.The horse hair is 2 times as thick as the human hair.
Explanation:
We have been given that Mateo is studying a human hair with a diameter of
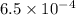 inches and a horse hair with a diameter of
inches and a horse hair with a diameter of
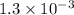 inches.
inches.
Since proportions states that two fractions are equal, So we will use proportions to solve our given problem.
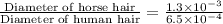
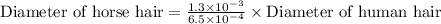
Now we will quotient rule of exponents to simplify our given problem.
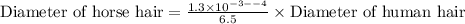
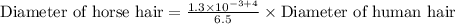

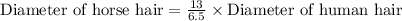
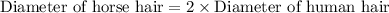
We can see that the diameter of horse hair is 2 times the diameter of human hair. Therefore, the horse hair is 2 times as thick as the human hair and option A is the correct choice.