Question

Rewrite the quadratic function in vertex form (which our OpenStax textbook also calls the standard form) and give the vertex. f(x)=x^2−7x

Answer 1

The vertex form of a quadratic equation follows the pattern below:

`f(x)=a(x-h)^2+k`

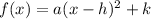
To convert our function here, f(x) = x² - 7x, to vertex form, here are the steps.

1. Isolate the terms that has the variable x. In this function, the terms that has the variables are already isolated.

2. Make sure the leading term has a numerical coefficient of 1. In this function too, our leading term that is x² already has a numerical coefficient of 1.

3. Do the completing the square process. In here, we will divide the second term 7 by 2 and then get the square. (7 divide by 2 = 3.5)(square of 3.5 = 12.25). Add this answer on both sides of the equation.

`f(x)+12.25=x^2-7x+12.25`

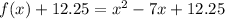
4. Factor the right side of the equation and equate the equation to f(x).

`\begin{gathered} f(x)+12.25=(x-3.5)^2 \\ f(x)=(x-3.5)^2-12.25 \end{gathered}`

We have reached the vertex form of the equation and it is f(x) = (x - 3.5)² + (-12.25).

Looking at the vertex form, the vertex (h, k) of this equation is (3.5, -12.25)