Question

Write the following inequality in slope intercept form. -6+2y less than or equal to 42

Answer 1

Answer: The required slpe-intercept form of the given inequality is

`y\leq 0* x+24.`

Step-by-step explanation: We are given to write the following inequality in the slope-intercept form :

`-6+2y\leq 42~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(i)`

We know that

the slope intercept form of a straight line with slope m and y-intercept c is given by

`y=mx+c.`

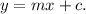
Writing equation (i) in slope-intercept form, we have

`-6+2y\leq 42\\\\\Rightarrow 2y\leq 42+6\\\\\Rightarrow 2y\leq 48\\\\\Rightarrow y\leq 24\\\\\Rightarrow y\leq 0* x+24,`

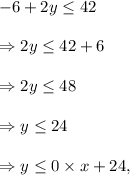
where slope, m = 0 and y-intercept, c = 24.

Thus, the required slpe-intercept form of the given inequality is

`y\leq 0* x+24.`

Answer 2

The slope intercept of a line is given by y=mx+c, where:
m=slope, c=y-intercept.
Thus the slope-intercept form of our equation will be:
-6+2y≤42
adding 6 in both sides we get:
-6+6+2y≤42+6
2y≤6
dividing both sides by 2 we get:
(2y)/2≤6/2
y≤3
the answer is y≤3