Answer
2. The Graph Contains The Point (5, 12)
Step-by-step explanation
Remember that in a linear function of the form
 ,
,
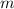 is the slope/rate of change of the line and
is the slope/rate of change of the line and
 is the y-intercept.
is the y-intercept.
From our equation we can infer that
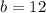 , so the y-intercept of our graph is 12 units above the origin on the point (0, 12). Therefore, choice 2 correctly describe the graph of y = 5x + 12
, so the y-intercept of our graph is 12 units above the origin on the point (0, 12). Therefore, choice 2 correctly describe the graph of y = 5x + 12
We can also infer that
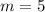 , so the slope of our line is 5, which is constant, so our line has a constant rate of change. Also, since every integer can be written as a fraction with denominator 1, we can write our slope as
, so the slope of our line is 5, which is constant, so our line has a constant rate of change. Also, since every integer can be written as a fraction with denominator 1, we can write our slope as
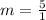 . Therefore, choices 1 and 2 correctly describe the graph of y = 5x + 12.
. Therefore, choices 1 and 2 correctly describe the graph of y = 5x + 12.
Now, remember that any point on the plane has coordinates
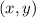 , so, to check if a point is on a line, we just need to replace the
, so, to check if a point is on a line, we just need to replace the
 and
and
 values in the line equation and check if the equation holds. Our point is (5, 12), so x = 5 and y = 12. Lets replace the values in our line:
values in the line equation and check if the equation holds. Our point is (5, 12), so x = 5 and y = 12. Lets replace the values in our line:
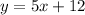
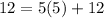
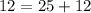
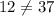
Since the equation equation doesn't hold (12 is not equal 37), we can conclude that the graph doesn't contain the point (5, 12). Therefore, choice 2 does NOT correctly describe the graph y = 5x +12.