Question

A carnival game allows a group of players to each draw and keep a marble from a bag. The bag contains 5 gold marbles, 25 silver marbles, and 70 red marbles. A player wins a large prize for drawing a gold marble and a small prize for drawing a silver marble. There is no prize for drawing a red marble. At the start of the game, the probability of winning a large prize is 0.05 and the probability of winning a small prize is 0.25. Suppose that the first player draws a silver marble and wins a small prize. What is the probability that the second player will also win a small prize? If a group of four plays the game one at a time and everyone wins a small prize, which player had the greatest probability of winning a large prize? How could the game be made fair for each player? That is, how could you change the game so that each player has an equal chance of winning a prize?

Answer 1

The probability is now .24

The first player had the highest probability of getting a silver marble

The game could be made fair by adding back the marble that was drawn after each draw

Answer 2

Answer with explanation:

It is given that:

The bag contains 5 gold marbles, 25 silver marbles, and 70 red marbles.

Ques 1)

We are asked to find the probability that the second player will also win a small prize given that the first player wins a small prize.

That is we need to find the conditional probability.

Let A denote the event that first player wins the small prize.

B denote the vent that the second player wins the small prize.

A∩B denote the event that both the player wins the small prize.

Let P denote the probability of an event.

We are asked to find:

P(B|A)

`P(B|A)=(P(B\bigcap A))/(P(A))`

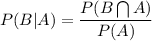
Now we know that:

`P(A)=(25)/(100)`

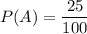
( Since out of 100 marbles 25 are silver)

Also,

`P(A\bigcap B)=(25_C_2)/(100_C_2)\\\\\\P(A\bigcap B)=(25* 24)/(100* 99)`

Hence,

`P(B|A)=(24)/(99)`

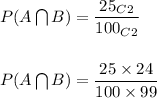
Hence, the probability that the second player will also win a small prize is:

0.242424

Ques 2)

The probability that the first player will win a large prize is:

5/100

( But the first player draws a silver marble and wins)

The probability that the second player will win a large prize is:

5/99

( Since one marble has been taken out by the first player so the second player is left with 99 choices and here also the second player draws a silver and wins the game)

Similarly,

The probability that the third player will win a large prize is:

5/98

( Since one more marble has been taken out by the second player so the third player is left with 98 choices and here also the third player draws a silver and wins the game)

The probability that the fourth player will win a large prize is:

5/97

Hence, the greatest probability of winning a gold marble is by:

Player 4. ( Since, 5/97 is greater than the rest three probabilities)

Ques 3)

The game can be made fair for each player if all have the equal choices of drawing a marble and this can be done by replacing the marbles that have been drawn out by the previous player.