Question

A lawn sprinkler sprays water 8 feet at full pressure as it rotates 360 degrees. If the water pressure is reduced by 50%, what is the difference in the area covered?

Answer 1

check the picture below

so, if the pressure is halfed, then the radius covered would be halfed

now, if 64π is the 100%, what is 16π in percentage?


`\bf \begin{array}{ccllll} amount&\%\\ \text{\textemdash\textemdash\textemdash}&\text{\textemdash\textemdash\textemdash}\\ 64\pi &100\\ 16\pi &x \end{array}\implies \cfrac{64\pi }{16\pi }=\cfrac{100}{x}\implies \cfrac{4}{1}=\cfrac{100}{x}\implies x=\cfrac{1\cdot 100}{4}`

Answer 2

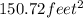`150.72 feet^2` is the difference in the area covered.

Explanation:

A lawn sprinkler sprays water 8 feet at full pressure, P.

A lawn sprinkler rotates 360 degree which means area covered by sprinkler is of circular shape. Since the sprinkler is in center and sprays the the water 8 feet away in all the direction while rotating.

Radius of the circle = 8 feet

Maximum pressure = P

As we know that higher the pressure higher will the force by which water will move out of the sprinkler. And with more force, sprinkler will able to spray water farther.

So we this we can say that pressure of the sprinkler is directly proportional to the radius of the circle in which water sprayed

`pressure\propto Radius`

`P\propto r`

`(P_1)/(r_1)=(P_2)/(r_2)=constant`

`P_1=P.P_2=P-50\%* P=0.5 P`

`r_1=8 feet.r_2=?`

`r_2=(0.5 P* 8 feet)/(P)=4 feet`

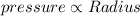
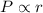
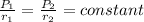
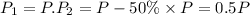
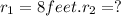
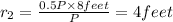
Area when ,
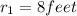`r_1= 8 feet` (Area of circle=
`\pi (radius)^2`)

`A=\pi r_1^(2)=\pi (8 feet)^2`

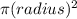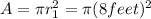
Area when ,
`r_2= 4 feet`

`A'=\pi r_1^(2)=\pi (4 feet)^2`

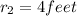
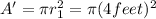
Difference in Area = A- A'

`\pi (8 feet)^2-\pi(4 feet)^2=\pi(48 feet^2)=150.72 feet^2`

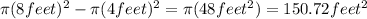
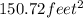`150.72 feet^2` is the difference in the area covered.