Question

Identify the initial value, the growth or decay factor, and the growth or decay rate of the exponential function below. f(x) = 2(94)* 13. Growth or decay 14. Initial value 15. Growth or decay factor 16. Growth or decay rate

Answer 1

the general expression of the growth function is :

`\begin{gathered} y=b(a)^x\text{ where b is the intial value, a is the growth rate} \\ \text{ and if x = +ve then the function is of growth} \\ \text{and if -ve then the fucntion is decaying} \end{gathered}`

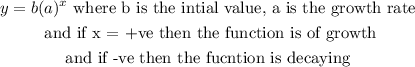
The given expression :

`f(x)=2(0.94)^x`

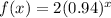
On comparing with the general equation :

b = 2

a = 0.94

Intial value = 2

As the variable x is positive so the functioni is Growth function

Growth factor is the factor by which a quantity multiplies itself over time.

So, here growth factor = 0.94 0r 94%

Growth rate is the addend by which a quantity increases (or decreases) over time.

so,

`\begin{gathered} f(x)=2(0.95)^x \\ f(x)\text{ for one year x = 1} \\ f(x)=2(0.95)^1 \\ f(x)=1.88 \\ \text{Growth rate= 1.88 + 2} \\ \text{Growth rate = 3.88} \end{gathered}`

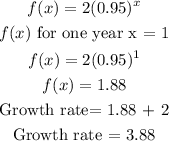
Answer :

13 ) Growth

14) 2

15) 0.94

16) 3.88