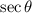Answer:
The simplified form of the given expression
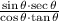 is
is
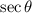
Explanation:
Given: Expression
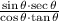
We have to writ the given expression in simplified form.
Consider , The given expression
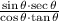
Since, we know,
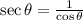
and
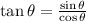
Substitute, we have,
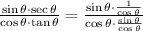
Simplify, we have,
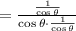
Simplify further, we get,
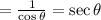
Thus, The simplified form of the given expression
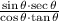 is
is