The exponential function is
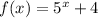
The polynomial function is

We want a value of x as such that
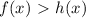
, so
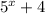
>
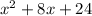
We are provided with four possible value of x. By process of trial and error, we will narrow down two values of x when the statement is changing from false to true
first, we try

by substituting into

and
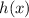
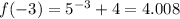
and

so

>
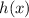
which is not the inequality wanted
We try
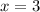
by substituting into

and
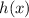
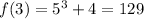
and
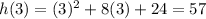
,
so

>
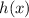
as wanted
We know that any values of

greater than three will give

greater than
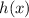
, so we narrow down to two values that make the statement changes from false to true.
There is one value between -3 and three that makes

greater than
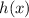
. From here we use the method of trial and error.
We can start with the mid value between -3 and three which is 0
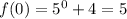
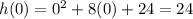

is less than
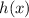
which isn't the inequality we want so here we narrow down the value of x must be between 0 and 3
We can try mid-value between 0 and three which is 1.5
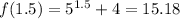
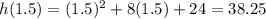

is still less than
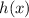
, so we now narrow down the value of x between 1.5 and 3
We try again using the mid-value between 1.5 and three which is 2.25
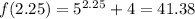
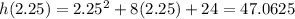
We still have

less than
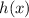
so we can narrow down further the value of x between 2.25 and 3 (which is quite a short interval already)
We can keep trying by choosing a value of x says x=2.6

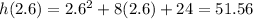
We have

greater then
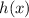
The narrowing down process continues where we now have the interval of x between 2.25 and 2.6. Keeping to one decimal place we can find the
value of x=2.4 is the approximate value where

is greater than
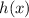
.
Answer: x=2.4