Answer:
The nth term for the geometric sequence is given by:
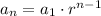
where,
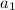 is the first term
is the first term
r is the common ratio of the terms.
As per the statement:
Given the sequence
-12,__,__, -324
here,
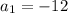 and
and

Solve for r:
By definition we have;

⇒
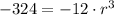
Divide both sides by -12 we have;
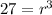
⇒
![r = \sqrt[3]{27} =\sqrt[3]{3^3} = 3](https://img.qammunity.org/2018/formulas/mathematics/high-school/w20lvvtg0vp4an7v4kbgv7ew7e6tlua6ep.png)
We have to find the missing terms
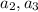
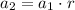
⇒
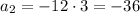
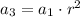
⇒

therefore, the missing terms in the following geometric sequence is,
-12,_-36_,_-108_, -324