Question

Rewrite 2x^2+13x+26/x+4 in the form q(x)+r(x)/b(x) . Then find q(x) and r(x).

Answer 1

Q(x)= 2x+5

R(x)= 6

Explanation:

Answer 2

We are dividing the polynomial
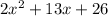
`2x^(2) +13x+26` by x+4

notice that
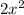
`2x^(2)` is x times 2x,

so if we multiply (x+4) by 2x, which gives us
`2 x^(2) +8x`, we can 'separate' one
`2 x^(2) +8x` from
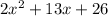
`2x^(2) +13x+26` to get the following simplification:


`(2x^(2) +13x+26)/(x+4)= ( 2x^(2)+8 x)/(x+4) + (5x+26)/(x+4)=2x+ (5x+26)/(x+4)`

similarly we notice that 5x is x times 5, so if we multiply (x+4) by 5, we get 5x+20 so we can rewrite


`(5x+26)/(x+4)= (5x+20)/(x+4)+ (6)/(x+4)=5+(6)/(x+4)`


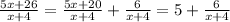
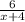
`(6)/(x+4)` can not be simplified any further since the degree of 6, is smaller than the degree of x+4

combining our work, we have:


`(2x^(2) +13x+26)/(x+4)=2x+5+(6)/(x+4)`

Answer:

q(x)= 2x+5
r(x)=6
b(x)=x+4


Remark: we can solve the problem by long division or the division algorithm as well.