Let:
P = Profit
n = Number of increments by $1
R = Revenue
The profit is given by:
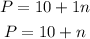
Therefore, the revenue is:
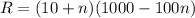
Expand the equation using the distributive property:
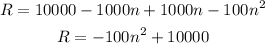
The maximum profit of this quadratic function is located at the vertex, we can find the vertex as follows:
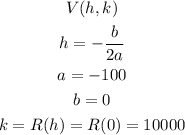
The vertex is (0,10000) in another words the maximum profit is achieve if you don't raise the price.