Answer:
No, it's not possible
Explanation:
We know that for various values of x ,
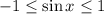
and

For values of
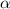 ,
,
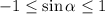
On multiplying all sides by 3, we get
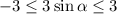
For values of
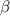 ,
,
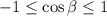
On multiplying all sides by 4, we get
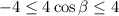
On adding all sides of
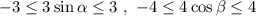 , we get
, we get
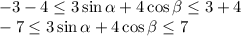
Therefore, maximum value of
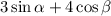 is 7.
is 7.
So, it's not possible that
