Solution:
Part A:
The image of the regular polygon given is an octagon.
An octagon is a polygon with 8 sides.
To calculate the area of a regular polygon, the polygon is split into triangles and the area of triangles is summed up to get the area of the polygon.

Therefore, the area of the regular polygon (octagon) is;
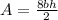
Part B:
To solve for the formula for the height h, we make h the subject of the formula;

Therefore, the height is;
