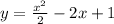The sketch of the parabola is attached below
We have the focus
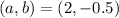
The point
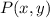
The directrix, c at
The steps to find the equation of the parabola are as follows
Step 1
Find the distance between the focus and the point P using Pythagoras. We have two coordinates;
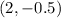
and
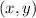
.
We need the vertical and horizontal distances to find the hypotenuse (the diagram is shown in the second diagram).
The distance between the focus and point P is given by
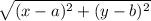
Step 2
Find the distance between the point P to the directrix

. It is a vertical distance between y and c, expressed as
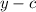
Step 3
The equation of parabola is then given as
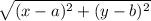
=
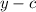
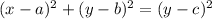
⇒ substituting a, b and c
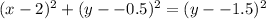
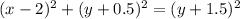
⇒Rearranging and making
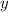
the subject gives