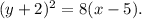Notice that the focus and the vertex of the parabola are on the line:

Therefore the parabola is a horizontal parabola.
Then, the directrix of the parabola is:
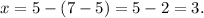
Now, recall that a parabola is a curve where any point is at an equal distance from a fixed point (the focus) and a fixed straight line (the directrix).
Therefore, (x,y) is on the graph of the parabola if:
![x-3=\sqrt[]{(x-7)^2+(y-(-2))^2}.](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/asxcxwpmkt0h8fwsvfl3.png)
Then:
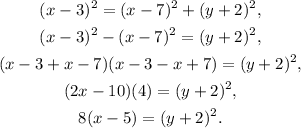
Answer: