The map of a biking trail is drawn on a coordinate grid. The trail starts at P(−3, 2) and goes to Q(1, 2). It continues from Q to R(1, −1) and then to S(8, −1). What is the tota…

Question

asked Nov 2, 2018 81.7k views

2 Answers

Kaushik Ghosh · Answer 1 · 2018-11-08T13:38:17+0000

Answer:

Total length of the biking trail is 14 units

Explanation:

The trail starts from point P(-3, 2) and touches points Q(1, 2), R(1, -1) and S(8, -1).

We have to calculate the total length of the biking trail.

Since distance between two points are represented by

d =
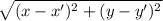
$\sqrt{(x-x')^(2)+(y-y')^(2)}$

So length of PQ =
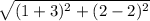
$\sqrt{(1+3)^(2)+(2-2)^(2)}$

PQ =
$\sqrt{(4)^(2)}$

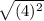
PQ = 4 units

QR =
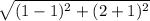
$\sqrt{(1-1)^(2)+(2+1)^(2)}$

QR =
$\sqrt{(3)^(2)}$

QR = 3 units

RS =
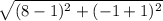
$\sqrt{(8-1)^(2)+(-1+1)^(2)}$

RS =
$\sqrt{(7)^(2)}$

RS = 7 units

Now total biking trail = PQ + QR + RS

= 4 + 3 + 7

= 14 units

Total length of the biking trail is 14 units