Question

When the function f(x) = 3(5)x is changed to f(x) = 3(5)x + 22, what is the effect? There will be no change to the graph because the exponential portion of the function remains the same. The y-intercept is 22 spaces higher. The x-intercept is 22 spaces higher. All input values are moved 22 spaces to the right.

Answer 1

The y-intercept is 22 spaces higher.  Adding a constant to a function shifts the parent function upwards by that number of units.

Answer 2

Answer: The y-intercept is 22 spaces higher.

Step-by-step explanation: Given function is
`f(x) = 3(5)^x`.

And transformed function equation
`f(x) = 3(5)^x + 22`.

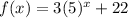We can see 22 is being added to the given function f(x) to get the transformed function.

Note: According to transformation rule, y = f(x) +k shift k units up.

22 is being added to the original function. So,
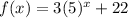`f(x) = 3(5)^x + 22` function would shift 22 units up that is y-intercept is 22 spaces higher.

Therefore , correct option is : The y-intercept is 22 spaces higher.