The height of the ball can be modeled by the equation:
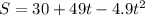
Where t is the time (seconds) after the ball is thrown.
The general form of the quadratic function is given by:
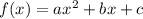
If you take a look, the equation can be written in this form:

Where a=-4.9, b=49 and c=30.
a. The vertex of the quadratic function is given by (h,k), where:
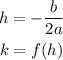
By finding h, you will obtain the t-coordinate of the vertex:
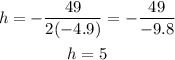
Thus, the t-coordinate of this quadratic function is t=5.
The S-coordinate of this quadratic function corresponds to the k-coordinate of the vertex: k=f(h). Then, let's evaluate the function in t=5:
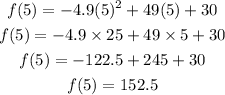
Thus, the S-coordinate of this quadratic function is S=152.5.
b. The vertex coordinates are (t, S)= (5, 152.5). It means that the ball reaches its maximum height (S) of 152.5 meters in a time (t) of 5 seconds. The answer is option D.
c. The function will be increasing until the ball reaches its maximum height (until the vertex), thus, it is increasing until t=5 seconds. After this time, the ball will start to fall. The answer is option A.