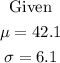
Part A: What percentage of years will have an annual rainfall of less than 44 inches?
First, solve for the z-score when x = 44 inches
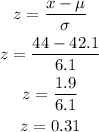
Next, find P(z < 0.31), by locating the probability to the left of the area of the z-table.
Multiply the probability by 100%

Rounding to the nearest tenth of a percent, the percentage is 62.2%.
Part B: What percentage of years will have an annual rainfall of more than 40 inches?
Solve for the z-score for x = 40 inches
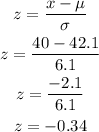
Next, find the area to the left of z-score, and subtract it from 1.
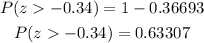
Multiply by 100%
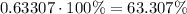
Rounding to the nearest tenth of a percent, the percentage is 63.3%.
Part C: What percentage of years will have an annual rainfall of between 39 inches and 43 inches?
Find the z-score for both x = 39, and x = 43
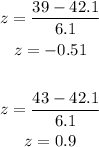
Find the area to the left of z-score.
Subtract 0.81594 by 0.30503, and multiply the result by 100%
[tex]\begin{gathered} P(-0.51Rounding to the nearest tenth of a percent, the percentage is
51.1%.