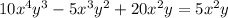Answer:

Explanation:
Given polynomial :
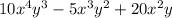
We can rewrite the terms given in the above polynomial as :-
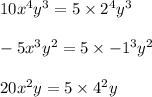
The highest common factor of numerical coefficients = 5
The highest common power of x =2
The highest common power of y =1
Therefore, the greatest common factor (GCF) of