Question

What are the net ionic equations for:

Ni(No3)2(aq) + Na2S(aq) = NiS(s) + 2 NaNo3(aq)
KBr(aq) + NaNO3(aq) = KNO3(s) + NaBr(aq)
Li2SO4(aq) + BaCl2(aq) = BaSO4(s) + 2 LiCl(aq)

Answer 1

1) Ni²⁺(aq) + S²⁻(aq) = NiS(s)

2) no

3) Ba²⁺(aq) + SO₄²⁻(aq) = BaSO₄(s)

Answer 2

Explanation :

In the net ionic equations, we are not include the spectator ions in the equations.

Spectator ions : The ions present on reactant and product side which do not participate in a reactions. The same ions present on both the sides.

(a) The given balanced ionic equation is,

`Ni(NO_3)_2(aq)+Na_2S(aq)\rightarrow NiS(s)+2NaNO_3(aq)`

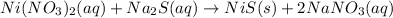
The ionic equation in separated aqueous solution will be,

`Ni^(2+)(aq)+2NO_3^-(aq)+2Na^+(aq)+S^(2-)(aq)\rightarrow NiS(s)+2Na^+(aq)+2NO_3^-(aq)`

In this equation,
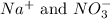`Na^+\text{ and }NO_3^-` are the spectator ions.

By removing the spectator ions from the balanced ionic equation, we get the net ionic equation.

The net ionic equation will be,

`Ni^(2+)(aq)+S^(2-)(aq)\rightarrow NiS(s)`

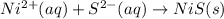
(b) The given balanced ionic equation is,

`NaNO_3(aq)+KBr(aq)\rightarrow KNO_3(s)+NaBr(aq)`

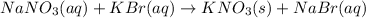
The ionic equation in separated aqueous solution will be,

`Na^+(aq)+NO_3^-(aq)+K^+(aq)+Br^-(aq)\rightarrow KNO_3(s)+Na^+(aq)+Br^-(aq)`

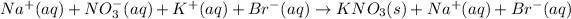
In this equation,
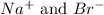`Na^+\text{ and }Br^-` are the spectator ions.

By removing the spectator ions from the balanced ionic equation, we get the net ionic equation.

The net ionic equation will be,

`NO_3^-(aq)+K^+(aq)\rightarrow KNO_3(s)`

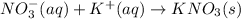
(c) The given balanced ionic equation is,

`Li_2SO_4(aq)+BaCl_2(aq)\rightarrow BaSO_4(s)+2LiCl(aq)`

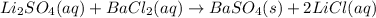
The ionic equation in separated aqueous solution will be,

`2Li^+(aq)+SO_4^(2-)(aq)+Ba^(2+)(aq)+2Cl^-(aq)\rightarrow BaSO_4(s)+2Li^+(aq)+2Cl^-(aq)`

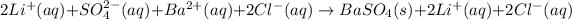
In this equation,
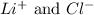`Li^+\text{ and }Cl^-` are the spectator ions.

By removing the spectator ions from the balanced ionic equation, we get the net ionic equation.

The net ionic equation will be,

`SO_4^(2-)(aq)+Ba^(2+)(aq)\rightarrow BaSO_4(s)`