Question

Upper a 18a 18?-footfoot ladder is leaning against a building. if the bottom of the ladder is sliding along the pavement directly away from the building at 22 ?feet/second, how fast is the top of the ladder moving down when the foot of the ladder is 44 feet from the? wall?

Answer 1

The foot of the ladder cannot be 44 feet from the wall, that would be larger than the length of the ladder, which means the ladder has crawled a few feet :)

So we are assuming a distance of 4 feet, similarly a rate of change in x equal to 2ft/s.

check the picture.

let
`h(x)= \sqrt{ 18^(2)- x^(2) } = (18^(2)- x^(2))^{ (1)/(2)}`

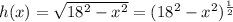
be the function of the height of the ladder with respect to x, the distance of the bottom of the ladder to the wall.

We want
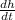
`(dh)/(dt)`, the rate of change of h with respect to t.

h is a function of x and x is a function of t, so we keep this in mind as we derivate h with respect to t:


`(dh)/(dt)= (dh)/(dx) (dx)/(dt)= (1)/(2) (18^(2)- x^(2))^{ -(1)/(2)}(-2x) (dx)/(dt)`

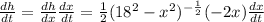
we substitute
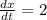
`(dx)/(dt)=2` and x=4:


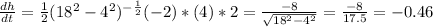
`(dh)/(dt)=(1)/(2) (18^(2)- 4^(2))^{ -(1)/(2)}(-2)*(4)*2= \frac{-8}{ \sqrt{18^(2)- 4^(2)} } = (-8)/(17.5)= -0.46` ft/s