Question

What is the simplest form of ^3 square root 27a^3b^7

Answer 1

`\bf \sqrt[3]{27a^3b^7}\quad \begin{cases} 27=3\cdot 3\cdot 3\\ \qquad 3^3\\ b^7=b^(3+3+1)\\ \qquad b^3b^3b^1\\ \qquad (b^2)^3b^1 \end{cases}\implies \sqrt[3]{3^3a^3(b^2)^3b^1} \\\\\\ 3ab^2\sqrt[3]{b^1}\implies 3ab^2\sqrt[3]{b}`

Answer 2

Option (a) is correct.

The simplified form of
`\sqrt[3]{27a^3b^7}` is
`3ab^2\sqrt[3]{b}`

Explanation:

Given :
`\sqrt[3]{27a^3b^7}`

We have to write the simplest form of given expression
`\sqrt[3]{27a^3b^7}`

Consider the given expression
`\sqrt[3]{27a^3b^7}`

27 can be written as 3³

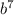`b^7` can be written as
`b^3b^3b`

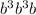
Thus, expression becomes,

`\sqrt[3]{27a^3b^7}=\sqrt[3]{3^3a^3b^6b^3b}`

Thus, Simplify, we get,

`=3ab^2\sqrt[3]{b}`

Thus, The simplified form of
`\sqrt[3]{27a^3b^7}` is
`3ab^2\sqrt[3]{b}`