Question

Find the coordinates of point Q that lies along the directed line segment from R(-2, 4) to S(18, -6) and partitions the segment in the ratio of 3:7.

Answer 1

(2 2/7, 5 1/3)

Explanation:

The coordinates of point Q, lies along R(-2,4) and S(18,-6)

thus, QR and RS, that is in ratio of QR : RS = 3 : 7

Let point Q = (x,y)

Hence, QR = -2 - x; RS = -6 - 4

Thus, QR/RS = 3/7, which is: (-2 - x)/(-6 - 4) = 3/7

7(-2 - x) = -30

-14 - 7x = -30

7x = 16

∴ x = 16/7 = 2 2/7

If x : y = 3 : 7 ( where x = 2 2/7)

Hence, (2 2/7)/y = 3/7

3y = 16

∴ y = 16/3 = 5 1/3

The coordinates of point Q = (2 2/7, 5 1/3)

Answer 2

find the distance between them
distance between (x1,y1) and (x2,y2) is

`D=√((x_2-x_1)^2+(y_2-y_1)^2)`

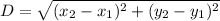
so distance between (-2,4) and (18,-6) is

`D=√((18-(-2))^2+(-6-4)^2)`

`D=√((18+2)^2+(-10)^2)`

`D=√((20)^2+100)`

`D=√(400+100)`

`D=√(500)`
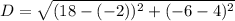
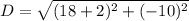
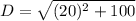
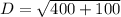
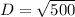
D=10√5

so in ratio 3:7
3+7=10
3/10 of 10√5 is 3√5

I'm thinkin you want R then Q then S such that RQ:QS=3:7
so
distance from R to Q is 3√5
Q is (x,y)
R is (-2,4)
D=3√5


`3√(5)=√((-2-x)^2+(4-y)^2)`

`3√(5)=√(x^2+4x+4+y^2-8y+16)`
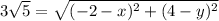
square both sides

`45=x^2+4x+4+y^2-8y+16`

`45=x^2+y^2+4x-8y+20`

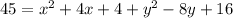
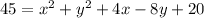
now, ithas to be on the line that R and S are on
do some simple math
slope is rise/run=-10/20=-1/2
y=-1/2x+b
4=-1/2(-2)+b
4=1+b
3=b
y=-1/2x+b

sub that for y in our other equation (
`45=x^2+y^2+4x-8y+20`)


`45=x^2+((-1)/(2)x+3)^2+4x-8((-1)/(2)x+3)+20`
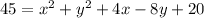
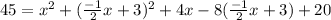
I'm too lazy to show you expanstion and whatnot so I'll give you the solution
we get (after some manipulation)
0=x²+4x-32
what 2numbers multiply to get -32 and add to get 4?
-4 and 8
0=(x-4)(x+8)
set to zero

0=x-4
4=x

0=x+8
-8=x
but wait, -8 is not between -2 and 18 so it can't be

so x=4

remember, y=-1/2x+3
sub that to get y=-1/2(4)+3=-2+3=1

the point is (4,1)
apologies for mishap