Question

A committee must be formed with 4 teachers and 5 students. If thereare 10 teachers to choose from, and 8 students, how many differentways could the committee be made?

Answer 1

We have to choose 4 teachers from 10 teachers.

So, the number of ways of doing this is

`10C_4=(10!)/(4!(10-4)!)=(10!)/(4!*6!)=(10*9*8*7*6!)/(4*3*2*6!)=10*3*7=210`

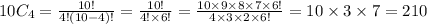
We have to choose 5 students from 8 students.

So, the number of ways of doing this is

`8C_5=(8!)/(5!(8-5)!)=(8!)/(5!*3!)=(8*7*6*5!)/(5!*3*2)=8*7=56`

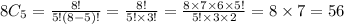
Now, we have to choose both teachers and students.

So the number of ways is

`10C_4*8C_5=210*56=11760`

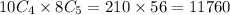
The different number of ways the committee made is 11760 ways.