Question

What is the simplest form of ^3√27a^3b^7

a 3ab^2(^3√b)

b 3ab^3(^3√ab)

c 9ab^2(^3√b)

d 9ab^3(^3√3ab)

Answer 1

`\displaystyle\\ \sqrt[3]{27a^3b^7} =\sqrt[3]{3^3 a^3b^6* b} =\sqrt[3]{3^3 a^3\Big(b^2\Big)^3* b} = \boxed{\bf 3ab^(\b2) \sqrt[\b 3]{\bf b} }\\\\ \text{Correct ansver: a)}`

Answer 2

Option a -
`\sqrt[3]{27a^3b^7}==3ab^2\sqrt[3]{b}`

Explanation:

Given : Expression
`\sqrt[3]{27a^3b^7}`

To find : What is the simplest form of expression ?

Solution :

Step 1 - Write the expression

`\sqrt[3]{27a^3b^7}`

Step 2 - Split the term into their factor,

`27=3^3`

`b^7=b^3b^3b`

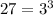
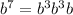
Step 3 - Re-write the expression,

`\sqrt[3]{27a^3b^7}=\sqrt[3]{3^3a^3b^6b^3b}`

Step 4 - Simplify the expression

`\sqrt[3]{27a^3b^7}==3ab^2\sqrt[3]{b}`

Therefore, Option a is correct.