Question

Points A, B, and C are collinear.What is the slope of AB in simplest form?2-43312B-4-3-2-112 3 423-4ابر بن ج

Answer 1

The slope between line A and B is 3/2

Explanation:

From the given graph, point A is (-3, -5) and point B is (1, 1)

From the given points

Let x1 = -3, y1 = -5, x2 = 1, and y2 = 1

The next step is to find the slope using the below formula

`\begin{gathered} \text{slope = }\frac{rise\text{ }}{\text{run}} \\ \text{rise = y2 - y1} \\ \text{run = x2 - x1} \\ \text{Slope =}\frac{y2\text{ - y1}}{x2\text{ - x1}} \end{gathered}`
`\begin{gathered} \text{Slope = }\frac{1\text{ - (-5)}}{1\text{ - (-3)}} \\ \text{slope = }\frac{1\text{ + 5}}{1\text{ + 4}} \\ \text{Slope = }(6)/(4) \\ \text{slope = }(3)/(2) \end{gathered}`

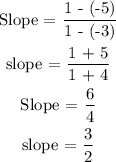
Therefore, the slope between line A and B is 3/2