Question

A) state the domain and range B)state the local minimum and maximum values and at which x they occur. You Can state these in point form. C) state the intervals of increase and the intervals of decreaseD) for what x values is f(x)<0 you Can estimate using decimals or fractions for x values that do not appear to be whole numbers

Answer 1

We are given the graph of a function and we are asked the following:

Part A. State the domain and range.

The domain of a function is the values of "x" that the function takes as input. Since from the graph we notice that the function takes all the values of "x", we say that the domain is:

`\text{dom f =}\mleft\lbrace x\in\R\mright\rbrace`

This means that the domain is all the real numbers.

The range of a function is the values of "y" that are outputs of the functions. Since we notice that the graph extends to infinity in both directions we can say that the range is:

`\text{range f =}\mleft\lbrace y\in\R\mright\rbrace`

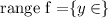
This means that the range of the function is all the real numbers.

Part B. The minimum and maximum values are the points where the graph has a tangent line of slope zero. From the graph we notice the following maximum point:

Therefore, the maximum point is located at x = -1. Also, from the graph we notice the following minimum point:

Therefore, the minimum point is located at x = 2.

Part C. The intervals of increase are the points where the values of "y" increase as the values of "x" increase. It can also be seen as the points where the slope of the lines tangent to the curve have a positive slope. From the graph we notice that the graph is increasing in the following intervals:

Therefore, the function increases from minus infinity to x = -1 and from x = 2 to infinity. We can write this in interval notation as follows:

`\text{Increase}=(-\infty,-1)\cup(2,\infty)`

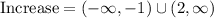
The function decreases when the slope of the tangent line is negative. From the graph we notice:

Therefore, the function decreases from x = -1 to x = 2. This can be written in interval notation as:

`\text{Decrease}=(-1,2)`

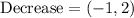
Part D. The function is f(x) < 0, when the graph is located under the x-axis. Therefore, the function is negative in:

Therefore, the function is negative from minus infinity to approximately x = -1.9 and from x = 0 to approximately x = 3.4.