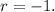Question

What are the values of a1 and r of the geometric series?

2 – 2 + 2 – 2 + 2

Answer 1

First term, a, is 2.  Next term, -2, is the product of 2 and -1 and is -2.  Next term, 2, is the product of -2 and -1.  Thus, the first term, a, is 2 and the common ratio, r, is -1.

Answer 2

Answer: For the given geometric series, the first term is
`a_1=2` and the common ratio is
`r=-1.`

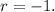
Step-by-step explanation: We are given to find the values of
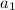`a_1` and
`r` of the following geometric series:

`2-2+2-2+2-~.~.~..`

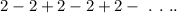
We know that

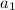`a_1` is the first term and
`r` is the common ratio of the given geometric series.

We can see that the first term of the given geometric series is 2.

So. we must have

`a_1=2.`

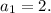
Also, common ratio is found by dividing a term by its preceding term.

Therefore, the common ratio
`r` of the given geometric series is

`r=(-2)/(2)=(2)/(-2)=~.~.~.~=-1.`

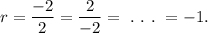
Thus, for the given geometric series, the first term is
`a_1=2` and the common ratio is
`r=-1.`