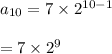Question

Given the sequence 7, 14, 28, 56, ..., which expression shown would give the tenth term? 7^10 7•2^10 7•2^9

Answer 1

7•2^9

Explanation:

This is a geometric sequence, since each term is found by multiplying the previous term by 2.

The explicit formula for a geometric sequence is given by

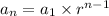`a_n=a_1 * r^(n-1)`, where a₁ is the first term and r is the common ratio, and n is the term number.

For our sequence, the first term is 7. The common ratio is 2. This gives us

`a_n=7 * 2^(n-1)`

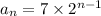
Since we want the 10th term,

`a_(10)=7 * 2^(10-1)\\\\=7 * 2^9`

Answer 2

each term is 2 times the previous
geometric series

an=a1(r)^(n-1)
an=nth term
a1=first term
n=which term
r=common ratio

common ratio is 2
first term is 7
n=10

so
7(2)^(10-1)
7(2)^9

last option is the answer